Scope:
The scope of the document includes basic nonlinear static analysis with geometry (large displacement) and material nonlinearity (elstoplastic) only. Contacts and Gaps are not part of the discussion. It is expected that the reader has basic knowledge about linear and nonlinear finite element analysis and basics of Nastran. Also, refer to Nastran Quick Reference Guide and Nastran Reference Manual – “Additional Topics” for detailed description of nonlinear static analysis
Introduction: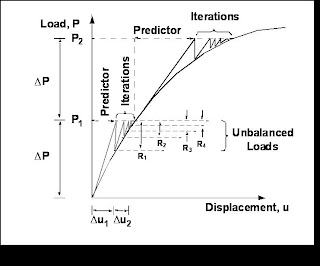
Nonlinear effects in structures occur mainly due to nonlinear material behavior and large deformations. All of these attributes may be represented by the availability of nonlinear elements. Non-linear elements may be combined with linear elements for computational efficiency if nonlinear effects can be localized.
Geometric nonlinearity becomes discernible when the structure is subjected to large displacement and rotation. Geometric nonlinearity effects are prominent in two different aspects: geometric stiffening due to initial displacements and stresses, and follower forces due to a change in loads as a function of displacements.
Material nonlinearity is an inherent property of any engineering material. Material nonlinear effects may be classified into many categories. They are plasticity, nonlinear elasticity, creep, visco elasticity.
The primary solution operations are gradual load or time increments (as shown by DP in Figure 1), iterations with convergence tests for acceptable equilibrium error (indicated by R1, R2 …) and stiffness matrix updates. The iterative process is based on the modified Newton’s method. The stiffness matrix is updated as per the selection of the iterative method (which has effect on computational efficiency). Solution sequence SOL 106 consolidates all the nonlinear features in MSC. Nastran.
General Solution Structure:$$----EXECUTIVE CONTROL SECTION----$$
SOL 106 $ NONLINEAR STATIC ANALYSIS
DIAG 8,50 $ DIAGNOSTIC PRINTOUT
CEND
$$----END OF EXECUTIVE CONTROL DATA----$$
$$----CASE CONTROL SECTION----$$
TITLE = TEST OF CTETRA ELEMENT (CUBE SUBJECT TO UNIAXIAL LOADING)
DISP = ALL
STRESS = ALL
SPC = 100
SUBCASE 1
SUBTITLE = ELASTIC -- LOAD TO 850. PSI
LABEL = LOAD TO YIELD
LOAD = 50
NLPARM = 50
SUBCASE 2
SUBTITLE = PLASTIC -- LOAD TO 1000. PSI
LABEL = LOAD BEYOND YIELD
LOAD = 100
NLPARM = 100
$$----END OF CASE CONTROL DATA----$
$$----BULK DATA SECTION----$$
BEGIN BULK
NLPARM 50 1 AUTO UPW NO $ PARAMETERS FOR NONLINEAR ITERATION OF SUBCASE 1
NLPARM 100 8 SEMI UPW NO $ PARAMETERS FOR NONLINEAR ITERATION OF SUBCASE 2
.
.
.
ENDDATANonlinear Characteristics & General Recommendation:
Modeling for nonlinear analysis is not exempted from the guidelines for good modeling practice pertaining to a linear analysis. Some of them can be summarized below:
Understanding the behavior of the structure. A simple model should be the starting point
Size of the model should be determined based on the purpose of the analysis balancing between the accuracy and efficiency of the analysis
Meshing biased towards the expected stress gradient, i.e. a finer mesh in the area of stress concentration
Avoid over stiff elements like TRIA3 and TET4
Other practices followed in general
Nonlinear analysis requires a better insight into structural behavior. First of all, the type of nonlinearities involved must be determined. The material nonlinear is significant depending on the magnitude and duration of the loading. The geometric nonlinearity is characterized by large rotations which usually cause large displacement
Linear Subcase Vs Nonlinear Subcase: In a linear analysis, subcases represent an independent loading condition. Each subcase is distinct from all others. In a nonlinear analysis, the end of a subcase is the initial condition for the next subcase or in other words, Subcase 2 is a continuation of Subcase 1 and Subcase 3 is a continuation of Subcase 2 and so on... Nonlinear static analysis permits only one independent loading condition per run. However, this loading does not need to be constant in magnitude or in position. Loadings can vary from subcase to subcase. Since a nonlinear static analysis is path dependent, the geometric and material changes in subcases are cumulative.
NLPARM Entry: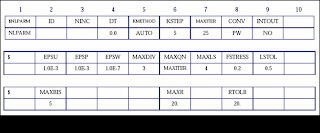
The unique data required for SOL 106 is supplied on the NLPARM entry, which controls the incremental and iterative solution processes. It is important that the most crucial data for successful nonlinear static solutions are contained in the NLPARM entry, which defines strategies for the incremental and iterative solution processes. It is difficult to choose the optimal combination of all the options for a specific problem. However, based on a considerable number of numerical experiments, the default option was intended to provide the best workable method for a general class of problems. Therefore, users with little insight or experience in a specific application should start with the default option.
Some important points in NLPARM entry:
The ID field is referenced by the NLPARM Case Control command.
The NINC field is an integer which specifies the number of increments to be processed in the subcase. The total load specified in the subcase minus the load specified in the preceding subcase is equally divided by this integer (NINC) to obtain the incremental load for the current subcase. Another subcase should be defined to change constraints or loading paths. However, multiple subcases may be required in the absence of any changes in constraints or loads to use a moderate value (e.g., not to exceed 20) for NINC. Use of a moderate value has advantages in controlling database size, output size, and restarts.
The DT field requires a real number specifying the time increment for each load step in the case of creep analysis. Not Applicable for current scope of discussion
Stiffness matrix update strategies are determined by a combination of the data specified in the two fields KMETHOD and KSTEP. Options for KMETHOD are AUTO, SEMI, or ITER. The KSTEP field, which is an auxiliary to the KMETHOD field, should have an integer equal to or greater than 1. Discussed in detail in a later section.
The MAXITER field is an integer representing the number of iterations allowed for each load increment. If the number of iterations reaches MAXITER without convergence, the load increment is bisected and the analysis is repeated. If the load increment cannot be bisected (i.e., MAXBIS is reached or MAXBIS = 0) and MAXDIV is positive, the best attainable solution is computed and the analysis is continued to the next load increment. If MAXDIV is negative, the analysis is terminated.
The convergence test is performed at every iteration with the criteria specified in the CONV field. Any combination of U (for displacement), P (for load), and W (for work) may be specified. All the specified criteria must be satisfied to achieve convergence.
INTOUT controls the output requests for displacements, element forces and stresses, etc. YES: Gives all outputs at every increment No: Gives output at last increment or load step
The convergence tolerances are specified in the fields EPSU, EPSP, and EPSW for U, P, and W criteria, respectively. Default values of tolerances should be adhered to until there is a good reason to change them.
Nonlinear Iteration Method – METHOD: Since each nonlinear problem is different, it is difficult to generalize the selection of an iteration solution method. In nonlinear static (SOL 106), the AUTO, SEMI, and ITER methods are available. In addition, a number of convergence acceleration techniques (e.g., quasi-Newton, line search, bisection) exist to enhance the nonlinear solution convergence. Each of the methods examines the appropriate parameters, convergence criteria, and error indicators to proceed through the solution.
The AUTO method works very well as a starting point and is the default method in the nonlinear static solution. This method essentially examines the solution convergence rate and uses the quasi-Newton, line search and/or bisection methods to perform the solution as efficiently as possible sometimes without a stiffness matrix update. Highly nonlinear behavior in some cases may not be handled effectively using the AUTO method.
The SEMI method is also an efficient technique for nonlinear static iteration. It is similar to the AUTO method since it uses the quasi-Newton, line search and/or bisection methods, but it differs from the AUTO method in one respect. The SEMI method forces a stiffness matrix update after the first iteration of a load increment. This update is performed irrespective of the convergence status of the solution. It is effective in many highly nonlinear problems where regular stiffness matrix updates help the solution to converge.
The ITER method is known as the "brute force" method in nonlinear static analysis because a stiffness matrix update is forced at every KSTEPth iterations with a resultant increase in CPU time. Its best applications tend to be those involving highly nonlinear behavior for which using only multiple iterations may not be efficient.
Load Step Bisection – MAXBIS and Convergence Criteria – CONV:
The incremental load value is bisected automatically if the convergence is not achieved in any incremental load step even after maximum number of iteration defined by the user. The allowable maximum number of bisections in each incremental load can be defined in the NLPARM card.
Hence, when the program reads that it is impossible for the solution to converge; a procedure called divergence processing is employed. One technique used in this procedure is bisection. Bisection means cutting the time step size or load increment size by half. This bisection occurs mainly due to any large nonlinearity in the model or when the NINC or load increment for the particular load step is too large. Divergence processing uses a combination of stiffness updates and bisections to facilitate convergence.
When the program determines that the large nonlinearity is gone and the solution is stabilized toward convergence, reversal of the bisection is performed in order to maintain the time step size required by the time step adjustment method given above.
Note: MAXBIS is not written out directly from Patran. It has to be manually included if the default values need to be overwritten
The activation of bisection method is indicated by the following message in the .f06 file:
*** USER INFORMATION MESSAGE 6187 (NCONVG)
*** BISECTION METHOD IS NOW ACTIVATED ***
The decision about the convergence criterion (CONV) to be used in the non-linear iterative solution strategy is important. Choice of convergence criterion depends on the type of structure, degree of accuracy required, efficiency in solution process required etc.
Convergence criterion may be any combination of out-of-balance forces, change in displacements, and energy (work) error. Convergence criterion based on out-of balance force and change in displacement is used before yielding and convergence criterion based on out-of-balance force is used after yielding because displacement is very high after yielding.
If a solution for particular load increment (or time step) cannot converge within MAXITER number of iterations, that increment is halved. Solution is attempted again, and if it does not converge again, another halving (bisection in NASTRAN speak) is done, up to a maximum number of bisections controlled by MAXBIS entry on NLPARM entry. Default is 5, max value is 10, but if you have to go higher, it most likely indicates either some irregularity with the model, or that NASTRAN is not the best tool for problem at hand.
A few suggestions worth trying for a solution to converge:
Increase NINC from default 10 to, say, 15
Increase MAXBIS, up to 10
Change KMETHOD to ITER and set KSTEP to 1 (caution: this will slow down the solution significantly)
Nonlinear Material Definition – MATS1 and TABLES1:
 Elastoplastic material consists of elastic and a plastic portion in stress-strain curve. The elastic portion is defined by providing the Young’s Modulus, E and Poisson’s ratio, n (MAT1); and the plastic portion is defined using a stress-strain curve data points through tabular input (MATS1 + TABLES1 or ‘FIELDS’ in Patran). A couple of important points to consider while defining stress-strain curve is that the first point must be at the origin (X1 = 0, Y1 = 0) and the second point (X2, Y2) must be at the initial yield point specified on the MATS1 entry. The slope of the line joining the origin to the yield stress must be equal to the value of E.
Elastoplastic material consists of elastic and a plastic portion in stress-strain curve. The elastic portion is defined by providing the Young’s Modulus, E and Poisson’s ratio, n (MAT1); and the plastic portion is defined using a stress-strain curve data points through tabular input (MATS1 + TABLES1 or ‘FIELDS’ in Patran). A couple of important points to consider while defining stress-strain curve is that the first point must be at the origin (X1 = 0, Y1 = 0) and the second point (X2, Y2) must be at the initial yield point specified on the MATS1 entry. The slope of the line joining the origin to the yield stress must be equal to the value of E.
Output in Nonlinear Static Analysis:There are two output blocks in SOL 106:
1) Nonlinear stress/strain (for non linear element only)
This is printed as "NONLI EAR STRESSES IN TETRAHEDRON SOLID ELEMENT S (TETRA)" in the *.f06 and it is given by default case control command NLSTRESS = ALL. The Patran stress output label NONLINEAR comes from this table. This is the "True stress." (This table also contains strains, the strains labeled NONLINEAR come from this output.) The nonlinear stress data is output in the element coordinate system.
 2) Linear stress/strain (for linear and nonlinear elements)
2) Linear stress/strain (for linear and nonlinear elements)
This is printed as "STRESSES IN TETRAHEDRON SOLID ELEMENTS (CTETRA)" in the *.f06 and it is given by default case control command STRESS = ALL. In Patran it is shown as "STRESS TENSOR". In short it is the "equivalent linear stress". You can also ask for STRAIN=ALL, this is the STRAIN TENSOR.
The stresses at center should match in both cases, however due to extrapolation, linear and nonlinear may not match. Many times the discrepancy is also caused by averaging stresses at node (in fringe plot)
And sometimes if you don’t have perfect elastic plastic the stresses could be higher than yield point as well. You can have a look at the "nonlinear stresses, stress tensor" with the centroidal values. It will give you the best correlation with hand calculations. [Nonlinear stresses are given for nodal as well as centroid]
Nastran nonlinear stress request (NLSTRESS) contains both - stress and strain. Whereas for linear elements (e.g.: CBAR), one has to request stress and strain separately (STRESS=ALL/STRAIN=ALL)
"STRESS TENSOR" is applicable for all the elements - (linear and nonlinear elements)
"NONLINEAR STRESSES, STRESS TENSOR" is applicable for nonlinear elements ONLY (e.g.: BEAM, TETRA (4&10)). "NONLINEAR STRESSES, EQUIVALENT STRESSES" is applicable to Von-Mises stresses in Non-Linear elements
"The results that you see marked as "Stress Tensor" in Patran from your nonlinear run are linear stresses based on nonlinear displacements, and the results marked as "Nonlinear Stresses, Stress Tensor" are the true nonlinear stresses. The ones marked "Nonlinear Stresses, Equivalent Stress" are a Von Mises stress calculation."
"STRAIN TENSOR" is same as stress tensor, but Strain Values - (for both linear and nonlinear elements). PLASTIC STRAIN is strain beyond the elastic limit.
When post-processing strain results in PATRAN, the results menu under "create Fringe plot" allows for two strain values the user can plot:
A) Nonlinear strains, plastic strain; and
B) Nonlinear strains, strain tensor
Choice "A" is consistent with the value from the .f06 file under the EFF. STRAIN/ PLAS/NLELAS column from the NLSTRESS case control request.
Choice "B" is consistent with the value from the .F06 file under STRAIN output you got from STRAIN=ALL case control command.
"The results that you see marked as "Stress Tensor" in Patran from your nonlinear run are linear stresses based on nonlinear displacements, and the results marked as "Nonlinear Stresses, Stress Tensor" are the true nonlinear stresses. The ones marked "Nonlinear Stresses, Equivalent Stress" are a Von Mises stress calculation."

Restriction and Limitations in SOL 106:
CROD, CBEAM, CGAP, CQUAD4, CQUAD8, CTRIA3, CTRIA6, CHEXA, and CTETRA elements may be defined with material or geometric nonlinear properties. All other elements will be treated as having small displacements and linear materials.
Constraints apply only to the nonrotated displacements at a grid point. In particular, multipoint constraints and rigid elements may cause problems if the connected grid points undergo large motions. However, also note that replacement of the constraints with overly stiff elements can result in convergence problems.
Large deformations of the elements may cause nonequilibrium loading effects. The elements are assumed to have constant length, area, and volume, except for hyperelastic elements.
Since the solution to a particular load involves a nonlinear search procedure, solution is not guaranteed. Care must be used in selecting the search procedures on the NLPARM data. Nearly all iteration control restrictions may be overridden by the user.
Follower force effects are calculated for loads which change direction with grid point motion.
Every subcase must define a new total load or enforced boundary displacement. It is necessary because error ratios are measured with respect to the load change.
Common Errors: Some of the common errors that can be avoided are:
Slope of elastic curve in MATS1/TABLES1 & Young’s Modulus, E in MAT1 should be same
Avoid having large load steps. E.g.: If the total load to be applied is say 10000N, break it into 2 or preferably 3 subcases/loadsteps
Since the units of convergence tolerance is independent of units, avoid tightening or loosening the tolerance in the first run
Make sure enough system resources (Memory and Hard Disk Space) are available at hand for large models
“User Fatal Message 4676 (NMEPD) - ERROR EXCEEDS 20.00 PERCENT OF YIELD STRESS IN ELEMENT ID=XX” may be encountered if there exists large deformation of the nodes of an element or presence of severely distorted elements. In case of large deformation (caused due to extremely large loads), then it is basically a large strain problem (as opposed to small strain assumption in Nastran) which needs to be solved by another solution sequence like MSC Marc or SOL 600. In case of severely distorted element, it is advisable to inspect the element quality in the mesh of the model.
“USER FATAL MESSAGE 1221 (GALLOC) - THE PARTITION OF THE SCRATCH DBSET USED FOR DMAP-SCRATCH DATABLOCKS IS FULL”. This fatal message is commonly encountered due to low system resources. Note that this fatal will stop writing the results into xdb/op2 completely and no output will be obtained. To avoid this fatal message, include “NASTRAN SYSTEM(151)=1” and increase the buff size “NASTRAN BUFFSIZE=65537” in the NASTRAN SYSTEM CELL SECTION of input file (above Executive Control Section)

 The unique data required for SOL 106 is supplied on the NLPARM entry, which controls the incremental and iterative solution processes. It is important that the most crucial data for successful nonlinear static solutions are contained in the NLPARM entry, which defines strategies for the incremental and iterative solution processes. It is difficult to choose the optimal combination of all the options for a specific problem. However, based on a considerable number of numerical experiments, the default option was intended to provide the best workable method for a general class of problems. Therefore, users with little insight or experience in a specific application should start with the default option.
The unique data required for SOL 106 is supplied on the NLPARM entry, which controls the incremental and iterative solution processes. It is important that the most crucial data for successful nonlinear static solutions are contained in the NLPARM entry, which defines strategies for the incremental and iterative solution processes. It is difficult to choose the optimal combination of all the options for a specific problem. However, based on a considerable number of numerical experiments, the default option was intended to provide the best workable method for a general class of problems. Therefore, users with little insight or experience in a specific application should start with the default option.
 2) Linear stress/strain (for linear and nonlinear elements)
2) Linear stress/strain (for linear and nonlinear elements)





